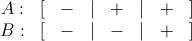转载自 Go Calf, 部分公式替换为图片。

之前在网上看到有好多人在讨论这道题，据说是一道Google的面试题。

问题描述：有两个长度均为 n 的整数数组 A 和 B，现在要从这两个数组中各抽出 s 个数字，分别构成两个新的数组 C 和 D，要求数组 C 和 D 的内积最大。

用数学语言描述一下题目:

当 s = 1 时，题目就退化成，从 n 个正整数中选取一个，从另外 n 个正整数中选取一个，使得乘积最大。显然，两次选取的都应该是那些数中最大的。

当 s > 1 时，我们分两步考虑，先考虑选取哪些数，再考虑这些数怎么配对。

1. 相信很多人都可以轻松地得出这样的结论：从 A 中选取最大的 s 个数构成 C，从 B 中选取最大的 s 个数构成 D，才有可能使得 C、D 内积最大。因为如果用A中的某个较小的数替换 C 中的任何一个数字，都会导致对应的乘积变小，从而整个内积变小。对于 D 也是类似的。

2. 对于选定的 C 和 D，如何配对呢？显然，应该让 C 中最大的数与 D 中最大的数相乘，C 中第二大的数与 D 中第二大的数相乘，以此类推。这个命题的证明也是很简单的，考虑任意两对数字：Ci < = Cj，Dk < = Dl，显然有

因此，如果 A、B 全部都是正整数，那只需要分别排序后，从大到小选取 s 个数即可。

只有负数跟只有正数是类似的，因为两个负数相乘的结果与这两个负数的绝对值相乘是一样的。根据上面的分析，我们只要对 A、B 分别排序后，从小到大（即绝对值从大到小）选取 s 个数即可。

再考虑两个数组一个全是正数，另一个全是负数的情况：

不妨设 A 中全是正数，B 中全是负数。

• 当 s = 1 时，题目就退化成，从 n 个正整数中选取一个，从另外 n 个负整数中选取一个，使得乘积最大。显然，两次选取的都应该是那些数中绝对值最小的（即最小的正数和最大的负数）。
• 当 s > 1 时，还是分两步考虑。

1. 很容易证明，应该从两个数组中分别选取绝对值最小的 s 个数（即正数数组中最小的 s 个数，负数数组中最大的 s 个数）。因为如果剩余的任何数字替换进来，都会导致对应的乘积的绝对值变大，乘积本身变小，从而整个内积变小。值得注意的是，很多人在这里容易出错，他们没有考虑到乘积为负数时，绝对值越大，乘积本身越小。

2. 对于选定的 C 和 D，如何配对呢？根据上面【一、2.】中的式子可以知道，我们还是要让最大的那对数相乘，第二大的那对数相乘，……。这里需要注意，也是很多人容易出错的地方，最大的那对数是正数中的最大值（绝对值也最大）和负数中的最大值（绝对值最小）。与全是正数时不同的一点是，两个数组都是正数时，最大的那对数的乘积恰好也是最大的；但一正一负的时候，最大的那对数的乘积并不一定是最大，最小的一对数的乘积也不一定是最小，但他们累加起来一定是最大的。比如 [1, 2] 和 [-1, -2]，正确的配对应该是2 * -1 + 1 * -2 = -4，而不是1 * -1 + 2 * -2 = -5。

几种特殊情况都考虑完了，最后就是正负数任意混合的一般情况。根据上面的分析，我们终归是要对 A 和 B 分别排序的，排序之后将两个数组的下标对齐，可以将两个数组分成三个部分，第一个部分中两个的数组元素都是负数（负数部分），第二个部分中一个数组元素都是负数而另一个都是正数（异号部分），第三个部分中两个数组的元素都是正数（正数部分），如下所示：

由于负数部分和正数部分都产生正的乘积，我们需要同时考虑这两个部分。每次从这两个部分各选出绝对值最大的一对数，将乘积更大的那对从 A、B 中转移到 C、D 中，然后继续比较。

如果负数部分和正数部分都取完了，还缺 m 对数，那就从异号部分选取最小的 m 个正数，和最大的 m 个负数，对应配对即可。

def MinInnerProduct(A, B, n, s):
  if not len(A) == len(B) == n or not 0 <= s <= n:
    raise Exception('Invalid arguments.')
 
  A.sort()
  B.sort()
  (C, D, sum) = ([], [], 0)
  (i, j) = (0, n - 1)
 
  while len(C) < s:
    val1 = A[i] * B[i]
    val2 = A[j] * B[j]
    if val1 < 0 and val2 < 0:
      break
    if val1 >= val2:
      C.append(A[i])
      D.append(B[i])
      sum += val1
      i += 1
    else:
      C.append(A[j])
      D.append(B[j])
      sum += val2
      j -= 1
 
  j -= s - len(C) - 1
  while len(C) < s:
    C.append(A[i])
    D.append(B[j])
    sum += A[i] * B[j]
    i += 1
    j += 1
 
  return (C, D, sum)

算法的空间复杂度为 O(s)，即用来存储 C、D 的空间；时间复杂度为 O(n log n)。

• http://www.gocalf.com/blog/max-inner-product.html